A normal ruler with lots of markings on it is actually overkill, you can make do with a smaller number of markings and still be able to measure any distance smaller than the length if the ruler itself. -Alaric Stephen I was inspired by Alaric Stephen’s blogpost on minimal rulers to make a set of Optimal Sparse Rulers.. A complete sparse ruler is called maximal if there is no complete sparse ruler of greater length with marks. Complete minimal rulers of length 135 and 136 require one more mark than those of lengths 124-134, 137 and 138. A sparse ruler is called optimal if it is both minimal and maximal.

Prasacco 2 Pcs 6 Inch Architectural Scale Ruler, Small

Aluminium Raised Grip Cutting Ruler 30cm Metal Safety

Printable Minimalist Tab Ruler
Set Minimal Ruler Measure Related Vector Stock Vector (Royalty Free

Fidoo Woodworking Ruler 3Pcs Precision Pocket Metal Slide Rule Inch T

Minimal Ruler Stock Illustrations 2,173 Minimal Ruler Stock

minimal ruler stylish + minimal co
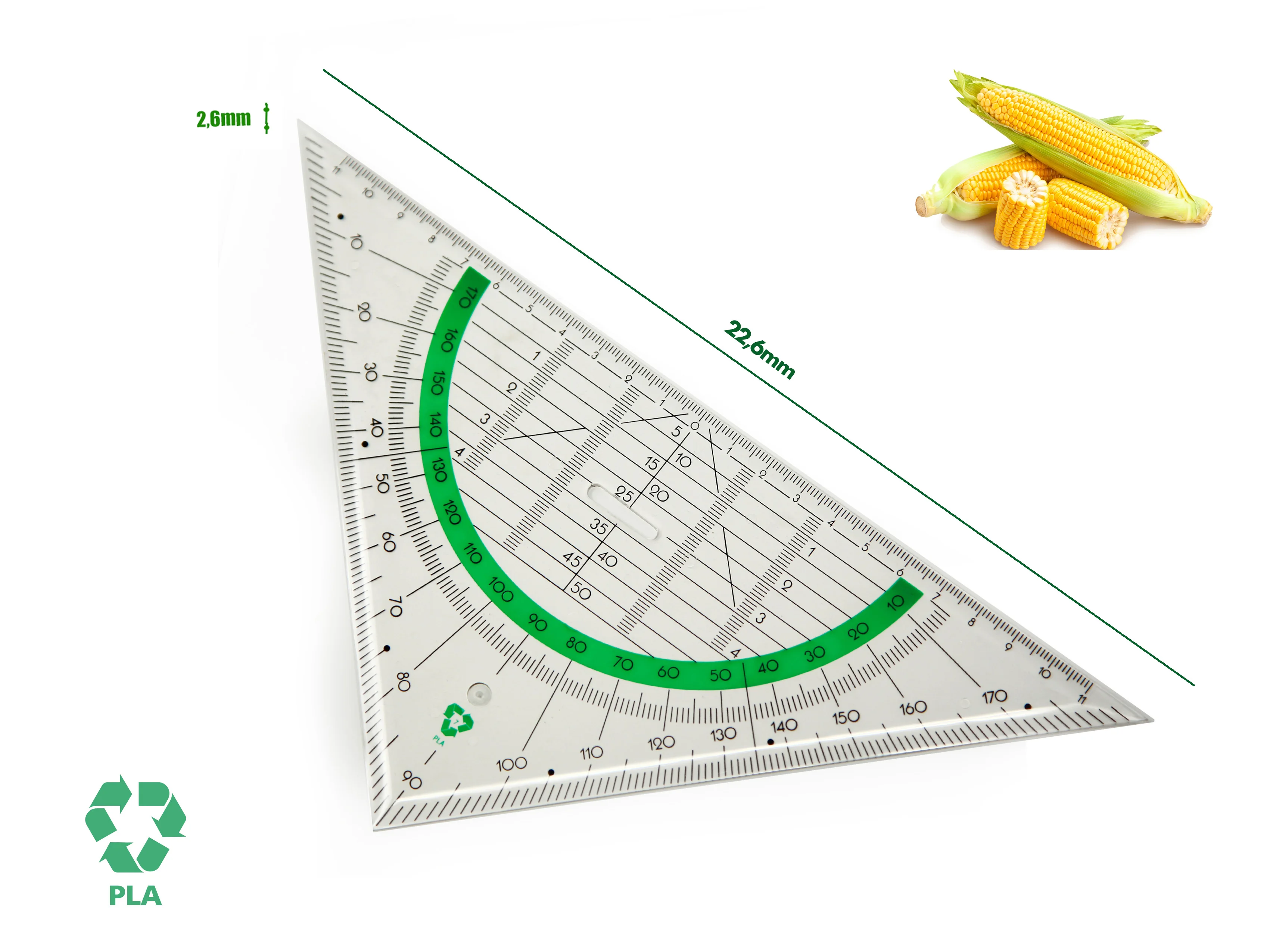
High School Trend 25cm Metal Ruler Transparent Pla Polylactic Acid

Product Ruler Guide

DSLSQD 4 Pieces Ruler Set Includes 12inch Straight Ruler

2 Pieces Flexible Ruler, 30cm/12inch Plastic Ruler

Eco Essential Pocket Organiser Filofax Filofax UK

3X 15 Fashion Design Ruler Cloth Design School Student

Sedf558732090465884d3f293396a9083G.jpg

Quickie Q50R Carbon Folding Powerchair

pencil and ruler illustration in minimal style 13395032 PNG

Transparent Triangular Ruler,Clear Acrylic Straight Ruler

Portable 6cm Small Copper Ruler 3mm Thickened Brass Metal Ruler

Metal Ruler with Cork Backed 30cm Straight Edge Ruler 12

gillian stevens Interior design minimal, Ruler set, Tiny space
:triangular_ruler: Jekyll theme for building a personal site, blog, project documentation, or portfolio. – mmistakes/minimal-mistakes. Sparse rulers A sparse ruler for length m, has less then n +1 marks but can still measure all lengths from 1 to n. A true sparse ruler is a sparse ruler that cannot measure length n +1, and a minimal sparse ruler is a sparse ruler where no mark can be removed. A ruler is defined by the ascending sequence P_1, .., P_k, where P_1 equals zero. The set of distances D({P_1, .., P_k}) which can be.